Generative Language Modeling for Automated Theorem Proving
1.论文信息
作者: Stanislas Polu, Ilya Sutskever
链接: https://arxiv.org/abs/2009.03393
OpenAI推出可以用于自动定理证明的GPT-f模型,其发现的新式简短证明有被收入Metamath函式库中,这是深度学习模型的定理生成证明首次被数学家接受,不过对此成果网友普遍保持中立,大佬认为没有特别之处1
也有网友对论文研究方法表示惊讶:「难以相信这种做法真的行得通。该研究的聪明之处在于将问题看作下一个证明步骤预测任务,然后进行采样。在掺杂了这么多非数学符号的文本上进行预训练竟能实现如此大的提升,真是太令人惊讶了。」2
2.论文摘要与简介
本文探索了基于transformer的语言模型在自动定理证明中的应用,提出了自动证明器和证明助手GPT-f并分析其性能。
学习证明定理与学习下围棋有一些相似之处:它们都提供成功决策的自动方式,也都是通过左右手互博的方式来自动地生成新数据。受到AlphaZero成功的启发,用神经网络进行推理学习用在自动证明领域中也许会大放异彩。
本文的贡献有:
1)验证了生成式预训练(generative pre-training)有效提高性能表现,并且在数学式的数据中(例如arXiv)预训练比在网络中通用文本数据中预训练更好。
2)模型大小与性能表现正相关
3)在语言模型生成的声明上迭代地训练价值函数是可以提升证明器性能表现的
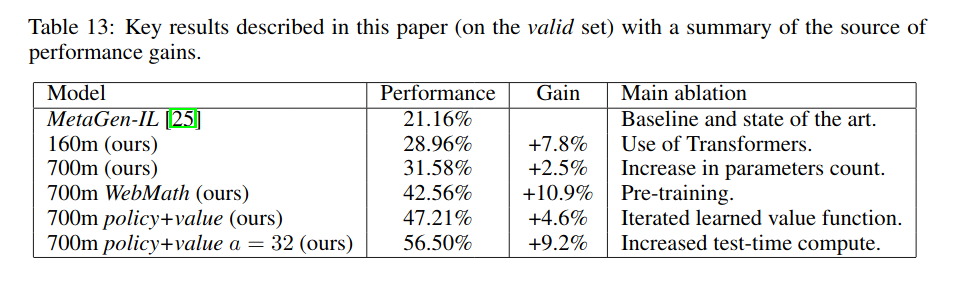
4)在Metamath环境中用最好的模型可以达到新的SOTA 56.22%(击败了现在的SOTA MetaGen-IL的21.16%),表明Transformer架构也许适合于形式推理
3.相关工作
1)Deep learning applied to premise selection and proof guidance
mainstream proof assistants still suffer from combinatorialexplosion of their search space as they are scaled to large corpuses, motivating the use of deep learning.Early applications of deep learning to formal mathematics focused primarily on premise selection and proof guidance. DeepMath explored the use of CNNs and RNNs to predict whether a premise is useful to demonstrate a given conjecture, their results were later improved with FormulaNet by the use of graph neural networks, reminiscent of NeuroSAT. Proof guidance consists in selecting the next clause to process inside an automated theorem prover.
2)Deep learning applied to automated theorem-proving
HOList proposes a formal environment based on HOL Light. They achieve their best performance with a GNN model designed for premise selection and the use of exploration. More recently, the same team studied the use ofthe BERT objective with Transformers on formal statements, demonstrating the potential of leveraging Transformers for formal reasoning. GamePad and CoqGymn/ASTactic introduce environments based on the Coq theorem prover.ASTactic generates tactics as programs by sequentially expanding a partial abstract syntax tree.Holophrasm and MetaGen-IL propose RNN-based models to generate proofs for Metamath (the formal system we focus on). They rely on three different models, one to value goals,one to select premises and one to generate substitutions.MetaGen-IL also demonstrates an uplift in performance by generating synthetic data by forward proving
3)Use of Transformers for symbolic tasks
Recently, Lample and Charton successfully applied Transformers to anti-derivative calculus and solving differential equations, hinting that Transformers are capable of generating the exogenous terms involved in the substitutions required for successful symbolic integration.The Universal Transformer, a Transformer with tied weights, was also shown to be successful at more algorithmic tasks.
4.本文模型
The main Metamath library is called set.mm, contains the background theorems required to demonstrate most Olympiad or undergraduate Mathematics type of problems.
1)Architecture
decoder-only Transformers similar to GPT-2 and GPT-3.The largest model has 36 layers and 774m trainable parameters.
2)Training Objective
The proofstep objective we use for training is a conditional language modeling objective that is asked to generate the PROOFSTEP given a GOAL, which is directly applicable to proof searches.
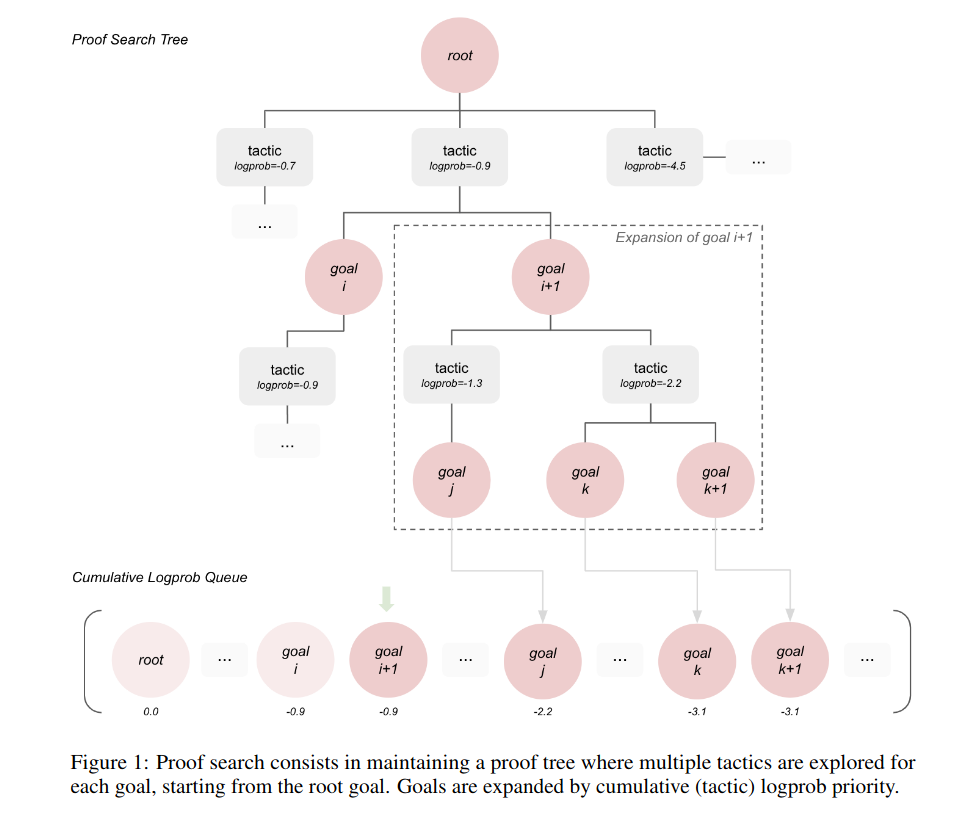
3)Proof Search
A proof search maintains a proof tree and a queue of open goals sorted by their cumulative logprob, initialized with the root goal that we wish to demonstrate.Intuitively we expand goals for which the generative model is the most confident globally. This has a tendency to explore breadth first as deeper goals have more parent tactics and therefore typically a higher cumulative logprob.
Each proof search involves d= 128 goal expansions, so proofs generated have at most d proof steps.When evaluating our models, we attempt a proof search for each statement in the valid set a= 4 times, starting from an empty proof tree each time. In the above,a,e, and d are hyperparameters of the search process that we can vary to achieve better performance (at the cost of more compute), but keep constant as we compare models.
Our implementation is capable of exporting our in-memory representations to both our JSON marshalled format and the official set.mm proof format. The latter allows us to verify the proofs we generate with an external Metamath kernel implementation such as mmverify.py or metamath-exe.Collectively, this proof search procedure and the formal verifier tied with it are what we refer to as the GPT-f automated prover.
We study the effect of pre-training on the performance of our models. We pre-train our models on both GPT-3’s post-processed version of CommonCrawl as well as a more reasoning-focused mix of Github, arXiv and Math StackExchange.
It is critical to ensure that our models are capable of proving at least basic technical theorems generally handled by high-level tactics in other systems (in domains such as arithmetic or ring equalities and inequalities).To achieve this goal we designed synthetic datasets allowing us to generate proofs for each of these domains at will while controlling precisely by how many proofs we augment our training set.
Our goal is to leverage these synthetic generators to ensure our models are confident when faced with such subgoals in order to mitigate the large number of proof steps they require.
The synthetically generated proofs account for approximately 1% of our training data which empirically appeared as big enough to achieve decent performance on the tasks we cared about and small enough not to hurt performance on the valid set, especially for small models. We attempted scaling the portion of synthetic proofs to 5% of the dataset and found out that it hurt performance for the model sizes we studied.
To achieve better performance, we also iteratively train a value function to guide the proof search, in place of the cumulative logprob priority described above.
This iterative training allows controlling for overfitting on both objectives by processing in the same way the data generated by proof searches on statements from the valid set and using the resulting datasets to track their associated valid loss.
5.实验结果
We fine-tune all of our models with 1024 examples per global batch and a context size of 2048 tokens,for at most 32B tokens (our augmented dataset contains∼1B tokens), early stopping at min valid loss when applicable. We anneal the learning-rate to zero (over 32B tokens). We found that restarting the training with an annealing to zero that matches the early-stopping for a given model only provides a marginal improvement, and avoided doing so.

This demonstrates the close (yet not perfectly correlated) relationship between sample complexity and performance in our formal reasoning setup, suggesting that sample complexity is an important driver of improved performance with formal mathematics.
GPT-fProof Assistant: We created an online proof assistant to allow interactive proof constructions with the assistance of our models.
6.结论
In this paper, we present the GPT-f automated prover and proof assistant and show that the Transformer is suitable to formal reasoning, achieving a new state of the art result on the Metamath library.In particular we demonstrate the importance of pre-training as well as iterative training of a value function. Our results suggest that tightly coupling a deep learning system with a formal system opens up interesting opportunities for further research, with the goal of better leveraging the generative power of the former and the verification capabilities of the latter.